Efectos geoespaciales en la modelización del precio de la vivienda en la ciudad de Madrid

El objetivo de este proyecto consiste en realizar una estimación fiable del precio de la vivienda en la ciudad de Madrid conocidos los atributos de cada inmueble. Este tipo de estudios ha sido ampliamente realizado en el ámbito de la econometría, sin embargo, muy poca literatura recoge la influencia de los efectos espaciales en el poder predictivo de las distintas modelizaciones al incorporar información geográfica.

Así, con el propósito de estudiar más en profundidad estos efectos, se proponen no solo modelos de regresión lineal múltiples, sino también desarrollos que introducen la posible autocorrelación espacial tanto en la variable dependiente como en los residuos del sistema. De este modo, se busca alcanzar una especificación óptima, cuyas predicciones puedan ser aplicadas en el mercado inmobiliario.

Antecedentes

Es posible, al trabajar con datos de corte transversal, encontrar los denominados efectos espaciales que se manifiestan a través de distintas dependencias entre observaciones con cierta proximidad geográfica. Estos efectos han sido ampliamente ignorados a lo largo de la historia por el hecho de que no pueden ser tratados por la econometría estándar, la cual se fundamenta en el análisis e interpretación de sistemas económicos con el fin de predecir variables tales como, por ejemplo, el precio de bienes y servicios.

Debido a la necesidad de resolver los problemas de origen geoespacial que la econometría estándar no puede solucionar, nació la econometría espacial, término acuñado por Paelinck y Klaassen y que hace referencia a las técnicas que tratan las consecuencias causadas por efectos espaciales en el análisis estadístico de modelos econométricos tradicionales. En las últimas décadas, la importancia y relevancia de este tipo de análisis ha ido en auge, debido, en parte, a las cada vez más accesibles y extensas bases de datos geo-referenciados, así como al incremento de la capacidad de computación de modelos cada vez más complejos.

Contexto

El mercado inmobiliario en España ha sufrido grandes altibajos durante las últimas décadas. Tras el mayor parón inmobiliario de la historia de España, producido en el año 2008, hubo un cambio de ciclo en el que los posibles compradores descendieron significativamente y además se tornaron más selectivos. La situación fue mejorando durante la década de los 2010, aunque a partir de 2020 se observa de nuevo una ralentización tanto en la subida del precio de la vivienda como en el volumen de compraventas. Este hecho parece indicar que pueda repetirse una situación similar a la de la crisis de 2008, en la cual el comprador sea reticente a tomar una decisión arriesgada y prefiera informarse adecuadamente.

Es, por tanto, el momento idóneo para proporcionar herramientas de análisis al comprador que le ayuden a tomar una decisión informada y acertada a la hora de adquirir una vivienda. Una herramienta de modelizado del precio del metro cuadrado como la propuesta en este proyecto, cuyas predicciones sean robustas ante efectos espaciales y, por consiguiente, aporten mayor fiabilidad, es justamente lo que el demandante de vivienda necesita. A su vez, también se trata de un valioso y potente recurso para el sector empresarial, ya que aporta beneficios tales como una correcta valoración o tasación de inmuebles, que además puede descomponerse por características y determinar la aportación de cada una de ellas al precio total de cada vivienda.

La ciudad de Madrid es, sin duda, una de las que más variabilidad presenta en el precio de la vivienda entre distritos o barrios, lo cual la convierte en una elección interesante para este tipo de análisis.

Base de datos

La extracción de la información del portal inmobiliario Idealista se ha llevado a cabo mediante un método de web scraping en el que se ha barrido cada uno de los 21 distritos de la ciudad de Madrid, de manera que se ha obtenido un total de 5935 observaciones (consultar el fichero de recopilación de inmuebles y extracción de características).

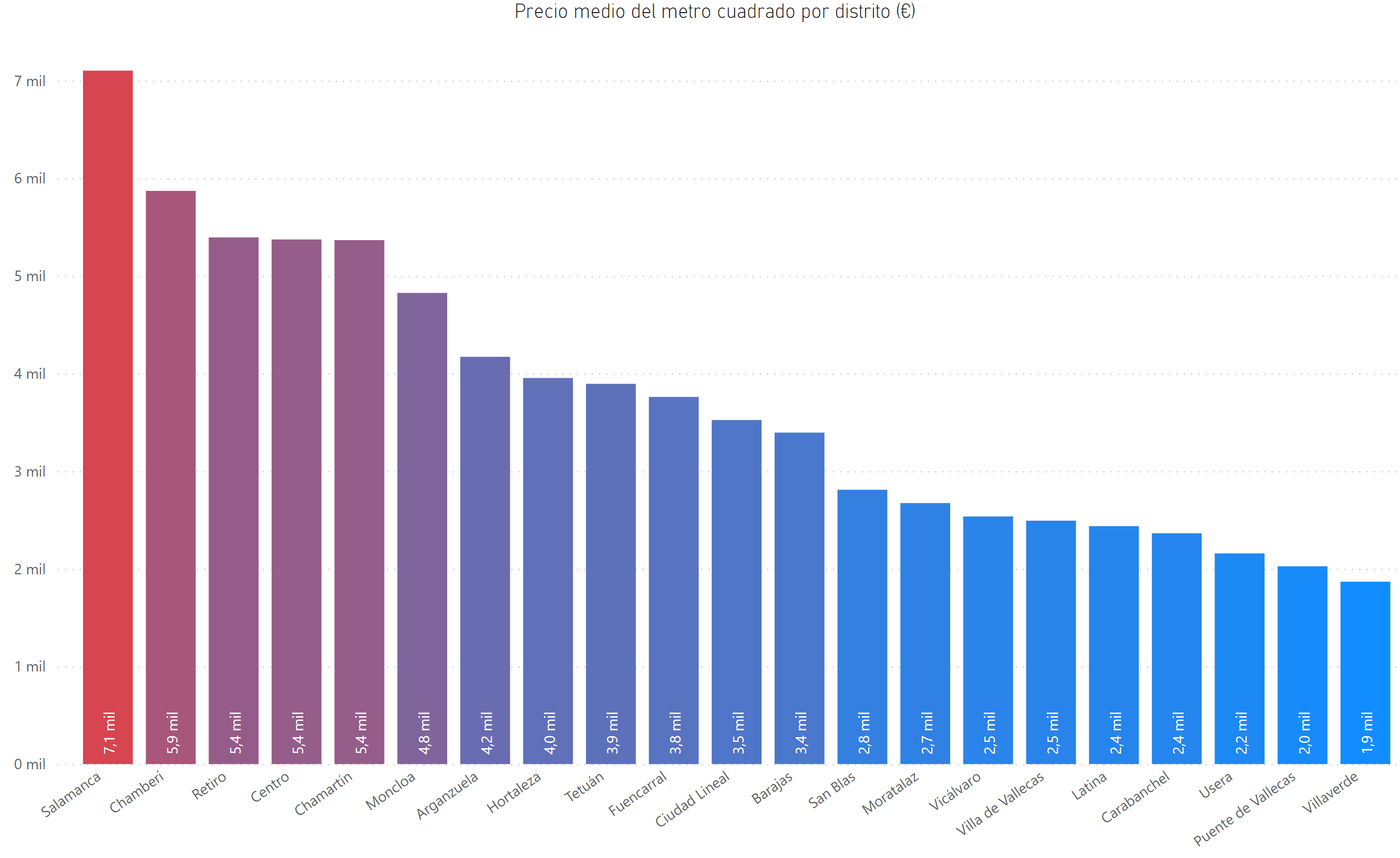
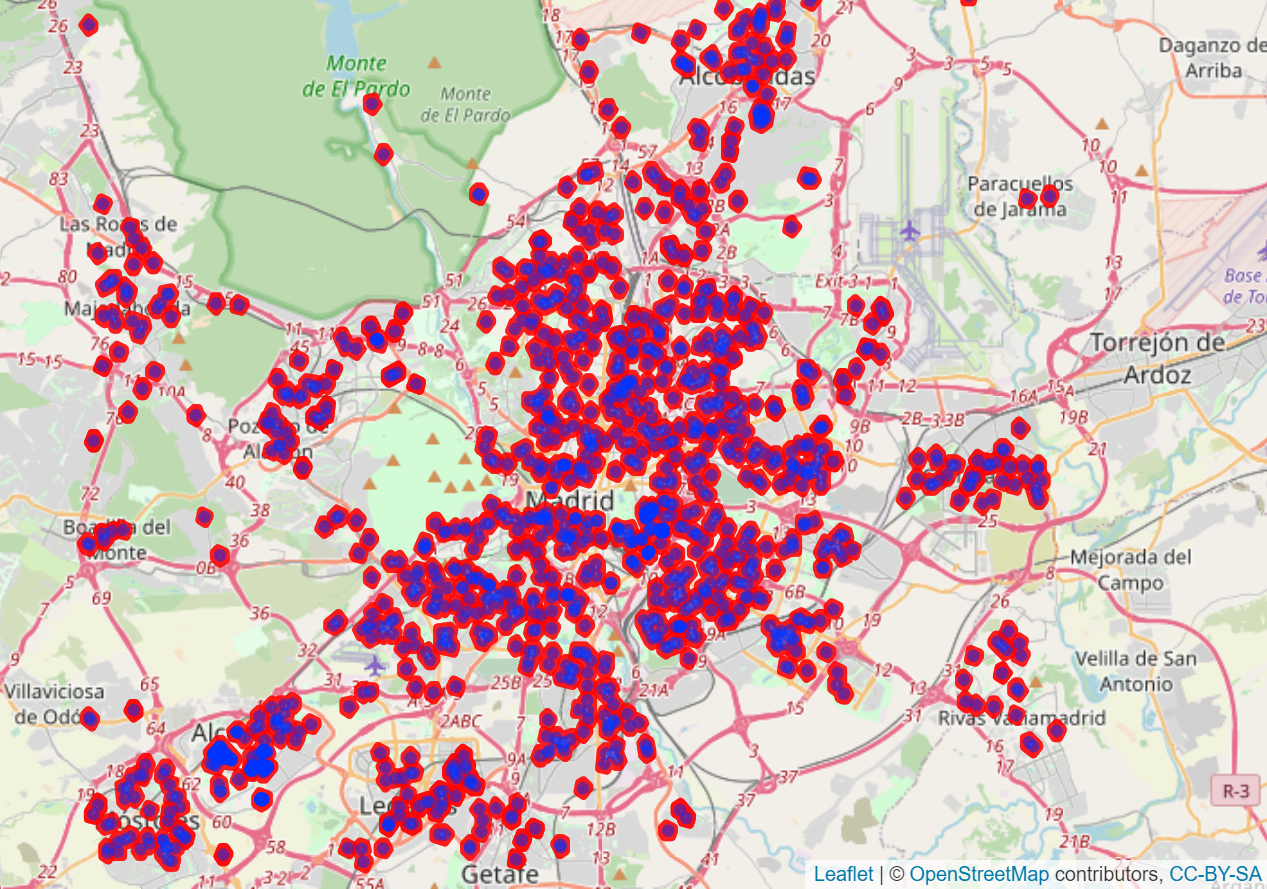
A partir de esta información, se puede conocer la distribución del precio de mercado por metro cuadrado de los inmuebles en los diferentes distritos. Como se puede observar, hay una diferencia del 380% entre el barrio más caro, el de Salamanca, y el más barato, Villaverde. La variabilidad puede observarse en el mapa de la figura.

Precio metro por distrito

Por otra parte, vamos a valernos del proyecto colaborativo OpenStreetMap para descargar información geográfica relevante (colegios, hospitales, etc.). La situación de los puntos de interés será incluida en nuestro conjunto de datos, permitiéndonos ponderar cada observación en relación a su proximidad a dichas localizaciones.

Para descargar polígonos se crea la siguiente función:

Descarga_OSM<-function(ciudad,key,value){
  
    #Descargo la Iformación
  mapa1 <- opq(bbox = ciudad)
  Poligonos_dentro <- add_osm_feature(mapa1, key = key, value = value)
  df <- osmdata_sp(Poligonos_dentro)
  #Centroides de cada polígono + representación
  spChFIDs(df$osm_polygons) <- 1:nrow(df$osm_polygons@data)
  centroides <- gCentroid(df$osm_polygons, byid = TRUE)
  names<-df$osm_polygons$name
  
  #Creo los Buffers de Hospitales. En menos de 200 metros. 
  buffer <- gBuffer(centroides, byid = TRUE, width = 0.002)
  
  #Convierto en Spatial Polygon DataFrame
  buffer <- SpatialPolygonsDataFrame(buffer, data.frame(row.names = names(buffer), n = 1:length(buffer)))
  #Combino los Polígonos que se entrecruzan
  gt <- gIntersects(buffer, byid = TRUE, returnDense = FALSE)
  ut <- unique(gt); nth <- 1:length(ut); buffer$n <- 1:nrow(buffer); buffer$nth <- NA
  for(i in 1:length(ut)){
    x <- ut[[i]];  buffer$nth[x] <- i}
  buffdis <- gUnaryUnion(buffer, buffer$nth)
  
  #Combino los Polígonos que se entrecruzan otra vez.
  gt <- gIntersects(buffdis, byid = TRUE, returnDense = FALSE)
  ut <- unique(gt); nth <- 1:length(ut)
  buffdis <- SpatialPolygonsDataFrame(buffdis, data.frame(row.names = names(buffdis), n = 1:length(buffdis)))
  buffdis$nth <- NA
  for(i in 1:length(ut)){
    x <- ut[[i]];  buffdis$nth[x] <- i}
  buffdis <- gUnaryUnion(buffdis, buffdis$nth)
  
  sd<-list(centroides,buffdis,names)
  
  return(sd)
  
}

Para descargar puntos se crea la siguiente función:

Descarga_OSM_points<-function(ciudad,key,value){
  q <- getbb(ciudad) %>%
      opq() %>%
       add_osm_feature(key, value)
  return(osmdata_sf(q))
}
mapa1 <- opq(bbox = "Madrid, Spain")

A continuación se incluyen las visualizaciones de los datos descargados, así como las variables calculadas a partir de los mismos:

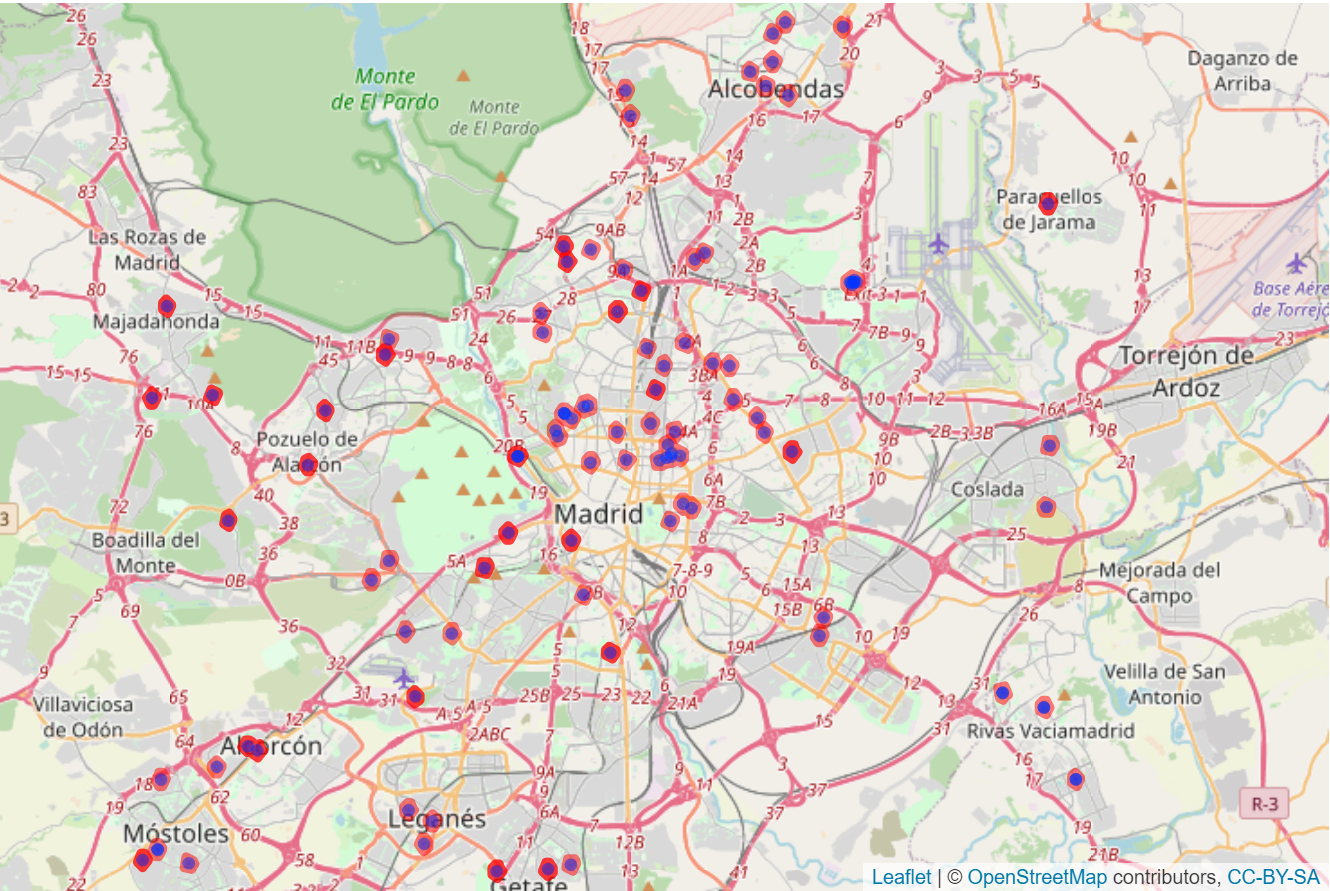
Hospitales

Hospitales<-Descarga_OSM(ciudad="Madrid",key='amenity',value = "hospital")

Mapa de hospitales

A partir de esta información se ha calculado la densidad de hospitales en un radio de 1km para cada vivienda.

#Hospitales
coordenadas<-as.data.frame(gCentroid(Hospitales[[2]], byid=TRUE)@coords)
Distancias<-distm(cbind(tabla$lon,tabla$lat),cbind(coordenadas$x,coordenadas$y),fun = distCosine )/1000
tabla$dist_hospital<-round(apply(Distancias,1,min),4)
tabla$dens_hospital<-apply((Distancias<1)*1,1,sum)

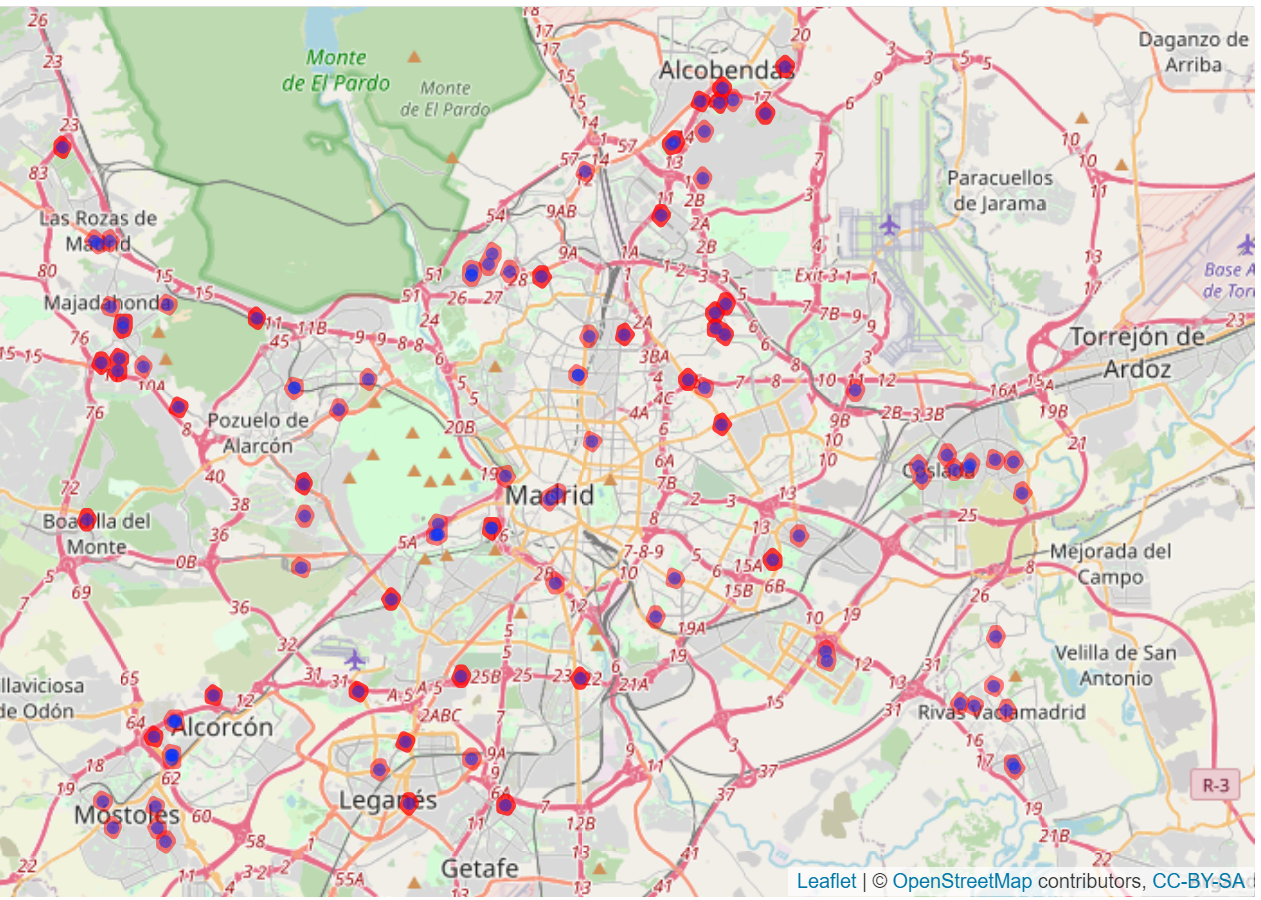
Centros comerciales

CentrosComerciales<-Descarga_OSM(ciudad="Madrid, Spain",key='shop',value = "mall")

Mapa de centros comerciales

A partir de esta información se ha calculado la densidad de centros comerciales en un radio de 1km para cada vivienda.

#CC
coordenadas<-as.data.frame(gCentroid(CentrosComerciales[[2]], byid=TRUE)@coords)
Distancias<-distm(cbind(tabla$lon,tabla$lat),cbind(coordenadas$x,coordenadas$y),fun = distCosine )/1000
tabla$dist_cc<-round(apply(Distancias,1,min),2)
tabla$dens_cc<-apply((Distancias<1)*1,1,sum)

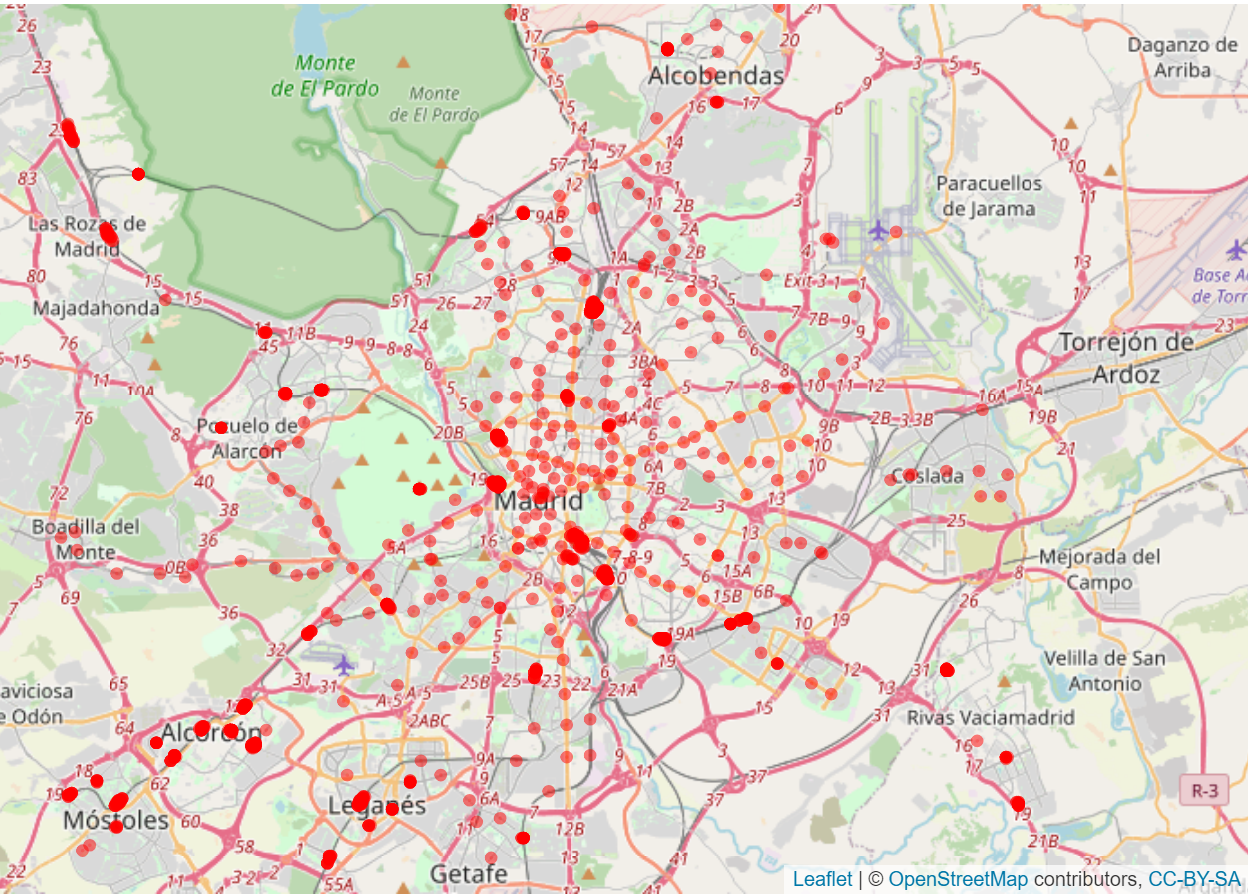
Transporte público

Metro<-Descarga_OSM_points(ciudad="Madrid", key='public_transport', value = "station")

Mapa de transporte publico

A partir de esta información se ha calculado la distancia más cercana a una estación de metro o de cercanías RENFE para cada vivienda.

#Metro
#coordenadas<-as.data.frame(gCentroid(Hospitales[[2]], byid=TRUE)@coords)
Distancias<-distm(cbind(tabla$lon,tabla$lat),cbind(coords_metro$lon,coords_metro$lat),fun = distCosine )/1000
tabla$dist_tp<-round(apply(Distancias,1,min),4)
tabla$dens_tp<-apply((Distancias<1)*1,1,sum)

Colegios

Colegios<-Descarga_OSM(ciudad="Madrid, Spain",key='amenity',value = "school")

Mapa de colegios

A partir de esta información se ha calculado la densidad de colegios en un radio de 1km para cada vivienda.

#Colegios
coordenadas<-as.data.frame(gCentroid(Colegios[[2]], byid=TRUE)@coords)
Distancias<-distm(cbind(tabla$lon,tabla$lat),cbind(coordenadas$x,coordenadas$y),fun = distCosine )/1000
tabla$dist_colegios<-round(apply(Distancias,1,min),4)
tabla$dens_colegios<-apply((Distancias<1)*1,1,sum)
head(tabla)

El código completo puede consultarse en este fichero, en el cual también se ha llevado a cabo la limpieza y preparación de la base de datos.

Hipótesis previas

Se procede a plantear las hipótesis preliminares para los algoritmos de predicción a implementar, siendo estos tanto interpretables como no interpretables. Asimismo, los distintos modelos predictivos serán juzgados tanto en base a sus respectivas bondades de ajuste como a través del análisis de sus residuos con la finalidad de determinar su idoneidad.

Regresión lineal múltiple (RLM)

Nuestro punto de partida será una regresión lineal múltiple, cuya forma funcional viene dada por:

$Y = \sum_{i=1}^k X_i \beta_i + \epsilon$

donde Y es la variable dependiente de interés (el precio de la vivienda), X_i son las variables explicativas del modelo, β_i es el coeficiente de regresión que mide la influencia de cada variable X_i sobre Y y ε es el error aleatorio.

Las principales hipótesis de este tipo de regresión son:

Linealidad en la relación entre X_i e Y.
Independencia entre las observaciones, entre las variables explicativas y entre los residuos del modelo.
Normalidad en la distribución de los residuos.
Homocedasticidad en los residuos.

En cuanto se viola una de las hipótesis, el modelo deja de ser óptimo y no podemos garantizar la fiabilidad de sus predicciones. En este caso, nuestro conjunto de datos está muy afectado por la dependencia espacial, lo cual se traduce en dependencias entre observaciones y heterocedasticidad en los residuos. Para hacer frente a este inconveniente, tomamos dos planteamientos alternativos:

Adición de variables espaciales con la intención de vencer la dependencia espacial.
Adición de no linealidades mediante modelos Multiadaptative regression splines (MARS).

Aun así, no esperamos lograr romper completamente los efectos espaciales, por lo que recurriremos a modelos más robustos en los que se añade un término de dependencia espacial, bien en la variable dependiente (modelos de retardo espacial), bien en los residuos (modelos de error espacial).

Modelos de retardo espacial (SAR)

Este tipo de modelos incluyen la correlación espacial en la variable dependiente y permiten a las observaciones en una determinada zona depender de observaciones en áreas vecinas. El modelo de retardo espacial básico se define como:

$Y=X\beta + \rho WY+\epsilon$

siendo $W$ la matriz de pesos espaciales, ε los errores independientes y ρ el nivel de relación autorregresiva espacial entre la variable dependiente y sus observaciones vecinas. Es decir, ρ es el impacto ‘‘boca a boca’’, lo cual quiere decir que las observaciones están impactadas por lo que sucede a su alrededor.

Resolviendo el sistema se obtiene:

$Y=(I-\rho W)^{-1}(X\beta +\epsilon) \to E[Y]=(I-\rho W)^{-1}(X\beta)$

De esta forma, esperamos obtener un ρ muy significativo, de manera que los residuos del sistema puedan considerarse independientes y, por tanto, estemos ante una mejor especificación del modelo.

Modelos de error espacial (SEM)

Como ya hemos argumentado, este tipo de modelos explican la dependencia espacial en el término de error o residual, es decir, el error lleva implícita una estructura espacial.

Se define como:

$Y=X\beta + e$

$e = \lambda W e + \epsilon$

donde W es la matriz de pesos espaciales, ε el término aleatorio de error y $\lambda$ es el parámetro autorregresivo.

Resolviendo el sistema:

$Y=X\beta + (I- \lambda W)^{-1} \epsilon$

En esta ocasión esperamos vencer por completo la heterocedasticidad de los residuos y, al igual que en el modelo SAR, lograr una muy buena especificación del sistema.

Modelos geográficamente ponderados (GWR)

Hasta ahora hemos definido modelos de regresión global general, en los cuales se tienen valores únicos de los parámetros β_i para todas las observaciones del conjunto de datos.

Con este tipo de modelizado, sin embargo, en lugar de tener un coeficiente global para cada variable, los coeficientes pueden variar en función del espacio. La idea fundamental es la medición de la relación entre la variable respuesta y sus variables explicativas independientes a través de la combinación de las diferentes áreas geográficas.

El modelo se define como:

$Y_s=\beta_{s1}X_1+\ldots+\beta_{s1}X_p+\epsilon$

siendo $s$ cada zona geográfica. Es decir, en el modelo ponderado geográficamente se tienen diferentes estimadores para cada una de las variables dependiendo de la localización.

Resolviendo el sistema:

$\beta_s=(X^tW_sX)^{-1}X^tW_sY$

Así, conseguimos reducir la dependencia espacial de los residuos del modelo, aunque no vamos a romper la heterocedasticidad de los mismos como veremos más adelante.

Gradient Boosting (GB)

El método de Gradient Boosting es una técnica de aprendizaje automático o Machine Learning que genera un modelo predictivo a partir de un conjunto de algoritmos de predicción débiles, típicamente árboles de decisión.

Al combinar weak learners de forma iterativa, el objetivo es que el algoritmo F aprenda a predecir valores minimizando el error cuadrático medio. De esta manera, en cada iteración el árbol de decisión se centra en disminuir los errores arrojados en la predicción previa. La predicción final se obtendrá a partir de la suma de todas las predicciones de los árboles de decisión implementados.

Al contrario de los modelos propuestos hasta ahora, el método de GB se trata de una técnica no interpretable, que además requiere de un gran esfuerzo en la parametrización o fine-tunning, de manera que no se caiga en un sobreajuste al conjunto de datos.

Evaluación de los modelos

A la hora de evaluar cada modelo y determinar su bondad de ajuste, vamos a apoyarnos fundamentalmente en cuatro validaciones:

Coeficiente de determinación ajustado. Su valor indica la proporción de variabilidad en la variable endógena explicada por el modelo en relación a la variabilidad total, ajustándose al número de grados de libertad:

$\bar{R}^2 =1 - \frac{n-1}{n-k-1} \frac{SS_{\text{res}}}{SS_{\text{tot}}}$

siendo n el tamaño de la base de datos, k el número de variables explicativas, SS_res la suma de residuos al cuadrado y SS_tot la suma total de cuadrados.
I de Moran. Este indicador proporciona una medida de la autocorrelación espacial, comparando el valor en una determinada área i en relación al resto de áreas. Su forma viene dada por

$I = \frac{N}{\sum_i \sum_j w_{ij}} \frac{\sum_i \sum_j w_{ij} (y_i - \bar{y}) (y_j - \bar{y})}{\sum_i (y_i - \bar{y})^2}$

siendo N el número de áreas consideradas, w_ij las componentes de la matriz de pesos espaciales y Y_i el valor de la variable Y en el área i.
Test de Jarque-Bera. Se trata de una prueba de bondad de ajuste para comprobar si una muestra de datos tiene la asimetría y curtosis de una distribución normal. Su forma es

$I = \frac{n}{6} \left ( S^2 + \frac{1}{4} (K-3)^2\right )$

donde n es el número de observaciones, S la asimetría de la muestra y K la curtosis.
Spatial Scan Statistics. Detecta y evalúa clusters en el espacio, permitiendo diferenciar si estos ocurren de forma aleatoria o siguen una distribución de probabilidad determinada. Para ello, se analiza gradualmente en intervalos espaciales si la variable en cuestión toma valores diferentes a los esperados.

En nuestro caso, usaremos la herramienta SatScan, un software especializado mediante el cual analizaremos los residuos de cada modelo, esperando que su distribución sea normal en cada región del espacio. Definimos estos intervalos espaciales usando círculos que contengan al 10\% de la población y cuyo centro esté localizado en cada una de nuestras observaciones. El programa se valdrá de simulaciones Montecarlo, obteniendo un p-value para cada región que no cumpla la distribución esperada.

Comparativa entre modelos

En esta carpeta se ha recopilado todo el código utilizado para el análisis y obtención de resultados de los distintos modelos. Para más información, puede contultarse el fichero Readme.

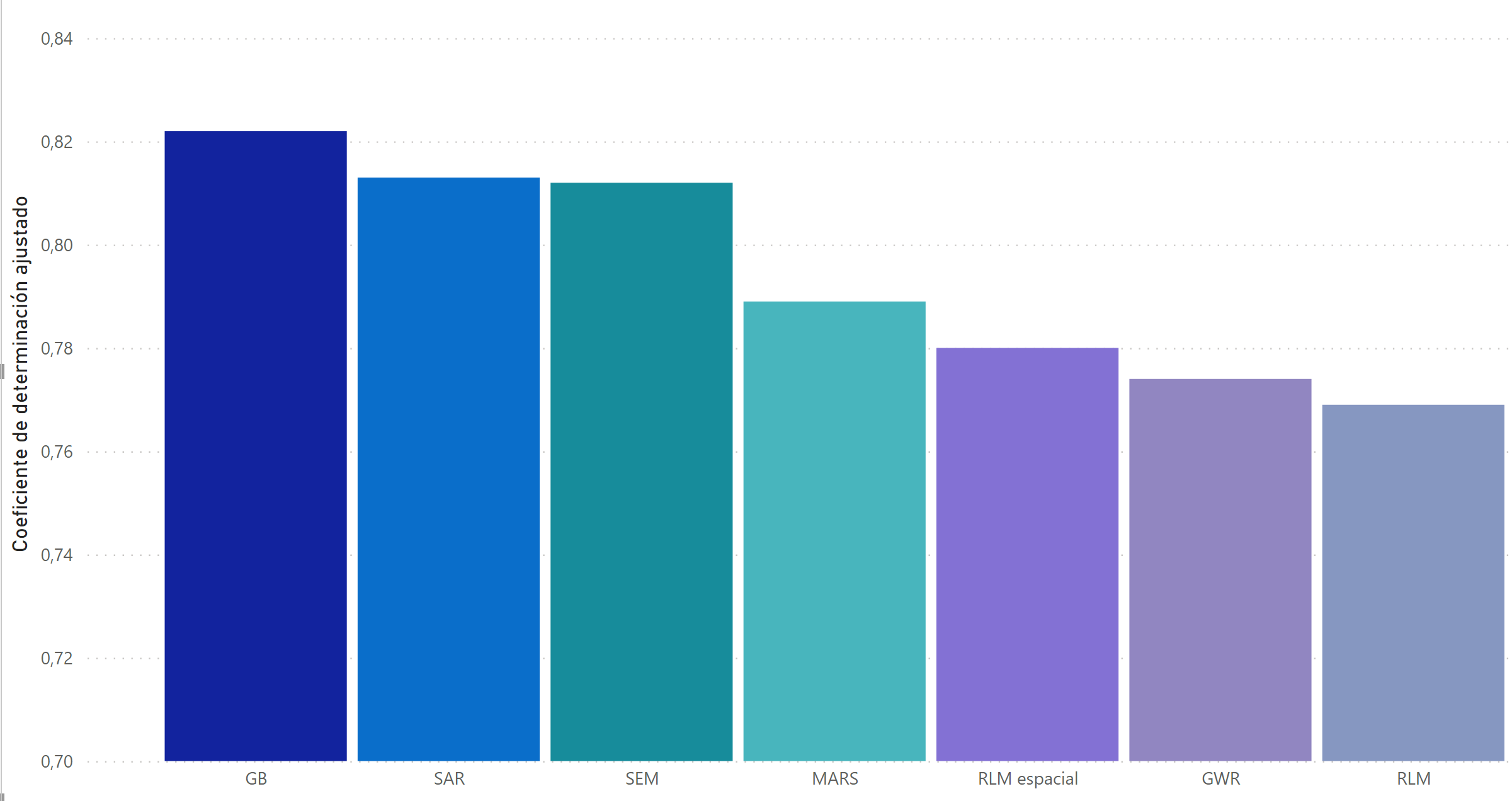
Como puede observarse a continuación, todos los modelos poseen un coeficiente de determinación ajustado superior al 75% sobre una base de datos de prueba, por lo que todos ellos proporcionan una explicación lo suficientemente buena de la variabilidad de la variable dependiente.

Comparativa_R2

En lo referente al poder predictivo de cada uno de ellos, es necesario diferenciar el modelo de Machine Learning, Gradient Boost, por tratarse de un algoritmo no interpretable. Así, si bien es el que mejores predicciones arroja de todos los modelos implementados, no tenemos conocimiento de cómo está contribuyendo cada variable, es decir, no se conoce el efecto marginal de cada atributo al precio final de la vivienda. En este sentido, se trata de una ‘‘caja negra’’ que puede no ser del todo conveniente si lo que se busca es entender cómo se ve afectado el valor de un inmueble en función de sus características.

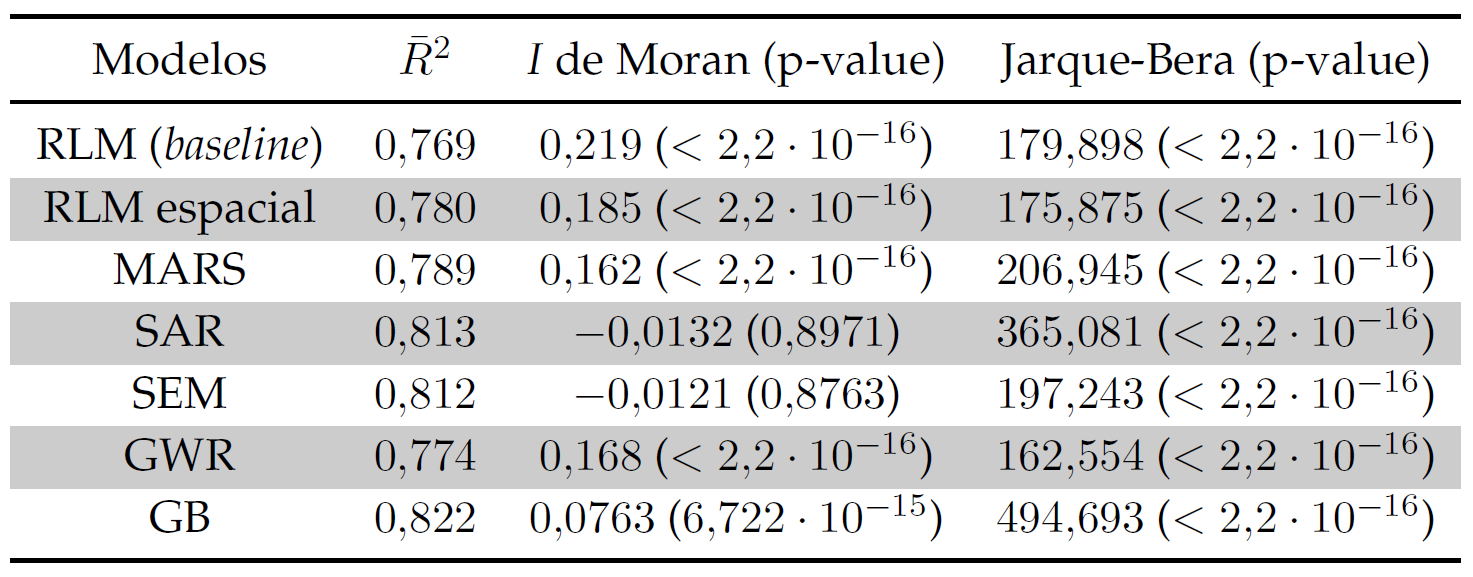
Si indagamos un poco más en los residuos, vemos lo siguiente:

Comparativa_final

Si recordamos, el objetivo de este proyecto consistía en implementar una correcta modelización del precio del metro cuadrado en la ciudad de Madrid, para lo cual se ha buscado romper tanto la heterocedasticidad como la dependencia espacial con el objetivo de arrojar predicciones robustas sobre futuras valoraciones de nuevos inmuebles. Con esta premisa en mente, por tanto, podemos descartar los modelos RLM, GWR y GB ya que que no cumplen con la meta que nos hemos propuesto. En efecto, atendiendo a los resultados de su I de Moran, ninguno de ellos es capaz de vencer los efectos espaciales, por lo que sus estimaciones serán en general sesgadas y poco fiables.

De entre las modelizaciones restantes, las cuales sí son interpretables, aquellas con mayor capacidad predictiva son el modelo de retardo espacial y el modelo de error espacial. Estos algoritmos sí que permiten conocer cómo afecta la variación de una variable independiente al resultado final, por lo que son una elección acertada en las situaciones en las que se requiera considerar este tipo de impacto sobre el precio de la vivienda.

Además, los modelos SAR y SEM sí consiguen deshacerse de los efectos espaciales puesto que un valor de los parámetros ρ y λ significativos implica un alto nivel de relación autorregresiva espacial entre la variable dependiente y sus observaciones vecinas. Es decir, se están incorporando satisfactoriamente los efectos espaciales en estos modelos. Este factor se ve recalcado mediante el resultado del test I de Moran, para el cual observamos un valor compatible con la hipótesis nula según la cual no existe dependencia espacial en los residuos. Por tanto, se concluye que los residuos no están autocorrelados espacialmente y se ha conseguido romper la dependencia espacial.

En concreto, a la hora de discernir cuál de los dos modelos es más apropiado, puede argumentarse que el poder de predicción del modelo SAR es ligeramente superior (0.5%), mientras que el modelo SEM parece eliminar más exitosamente la autocorrelación espacial. Por tanto, a priori no existen grandes disimilitudes entre ambos y la elección deberá realizarse basándose en las discrepancias entre resultados –de haberlas– al aplicarse sobre diferentes bases de datos.

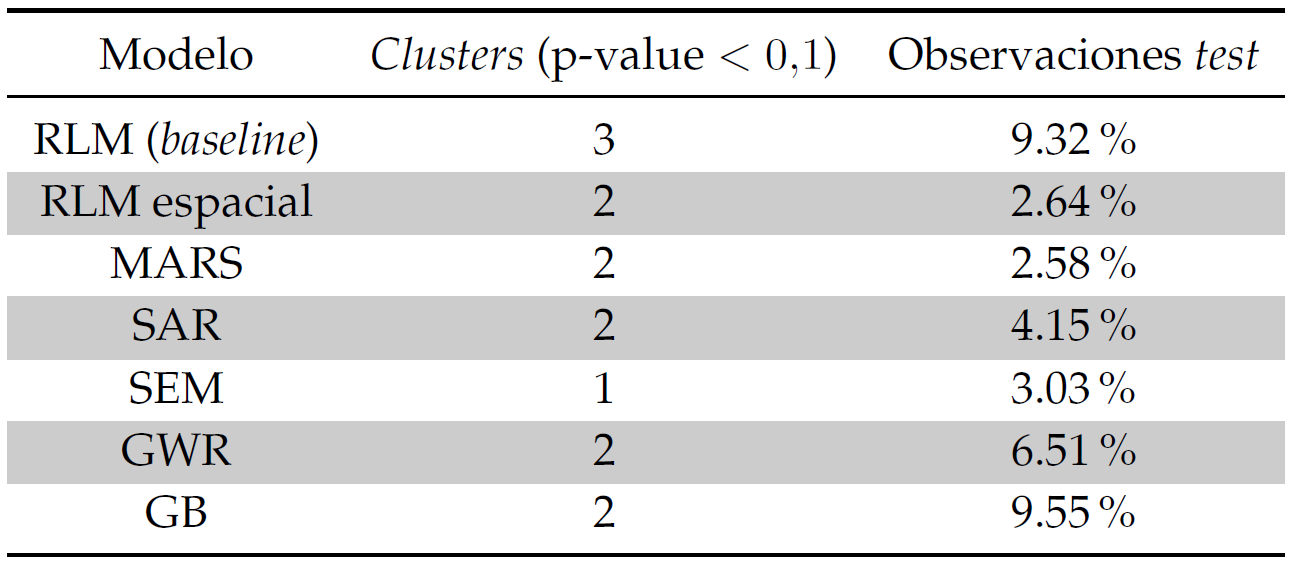
Por otra parte, es útil considerar la información recopilada en el siguiente cuadro, en el cual se muestran los resultados del análisis estadístico espacial realizado mediante la herramienta SatScan.

Comparativa_final SS

Conociéndose el número de clusters con p-value inferior al 10%, así como el porcentaje de población que estos representan y su distribución en el espacio, podremos discernir las zonas problemáticas para cada modelo. De esta forma, por ejemplo, para los modelos interpretables SAR y SEM se tiene que el centro de Madrid es probablemente más propenso a arrojar errores en la predicción, si bien el porcentaje total de la población que representan es bastante bajo (<5%). Así, las posibles causas de este efecto pueden ser las expuestas a continuación:

Omisión de variables relevantes. Pese a que nuestro modelo incluye la variable dist_centro (representando la distancia al centro de Madrid), así como los diferentes distritos en los que se halla cada piso, puede que la dimensión espacial no se esté teniendo en cuenta adecuadamente o haya más atributos relevantes en esta zona.
Mala especificación del modelo. Es posible que nuestro modelo no sea el adecuado para resolver este tipo de problema y, aunque se incluyan más variables explicativas, no se aprecie ninguna mejora significativa.
Problemas con la linealidad del modelo. Puede ocurrir que las variables presenten no linealidades precisamente en las regiones identificadas con SatScan.

En contraposición, el modelo no interpretable GB es menos fiable al sur y este de la ciudad, comprendiendo en este caso más del doble de observaciones con respecto al SAR y SEM (casi un 10%).

Conclusiones

A lo largo de este proyecto, se han propuesto varias modelizaciones para el desarrollo de una herramienta de tasación de inmuebles que puede ser aplicada en la ciudad de Madrid. Tras comprobar que las predicciones son robustas, especialmente para el modelo de error espacial (SEM), concluimos que los efectos espaciales juegan un papel importante y deben ser tenidos en cuenta si se quieren obtener resultados fidedignos que puedan ser posteriormente aplicados al mercado inmobiliario.

Pero, ¿por qué es tan importante incorporar este tipo de efectos? El hecho de que exista una autocorrelación espacial entre los residuos, tal y como indica el resultado obtenido en el test I de Moran, viola la hipótesis de independencia entre los mismos. Como consecuencia, los modelos lineales generados son poco fiables, puesto que los parámetros de regresión pueden estar sesgados, traduciéndose en una sobreestimación o subestimación de su poder predictivo. En concreto, esto significa que los precios de los inmuebles están interconectados, es decir, los pisos caros están cerca de los caros y viceversa. Ignorar este hecho puede acarrear graves consecuencias a la hora de generalizar el modelo y realizar nuevas predicciones, pues puede llevarnos a tomar decisiones erróneas debido al sesgo de la estimación.

Para saber más…

Todo el análisis recopilado en este repositorio se ha desarrollado como parte del Trabajo de Fin de Máster realizado en el Máster en Big Data & Data Science de la Universidad de Barcelona, colaborando con el Instituo de Formación Continua (IL3). El trabajo completo puede consultarse aquí.